What is a PID controller?

A PID controller is part of a feedback loop system used to keep a component in a system at a given value. In a motor controller a PID controller is used to keep motor speed or position where the user commands it. Outside conditions like increasing the load on a motor will cause it to vary from where it was set. The PID controller automatically corrects for these changes and brings the motor speed or postion back to the correct value.

Why use a PID controller?

In a system like a robot it is desirable and sometimes essential to be able to maintain values like motor speed or motor position to ensure the system operates properly. Wheeled robots need consistent and accurate speed to be able to drive straight, turn properly and account for changes in traction. Robotic arms need accurate and consistent positioning to be able to locate, grab and move objects. A PID controller helps to maintain these values over time.

How a PID controller works

A PID controller works by looking at the error between a parameter and what the parameter should actually be. It then tries to correct the error to bring it as close to zero as possible. Internally it looks at three aspects of the error and uses these together to correct the system. The three aspects are the proportional, the integral and the derivative. When tuning as PID controller you will be setting a numerical value to adjust how each of these components interacts with the system being cotrolled.

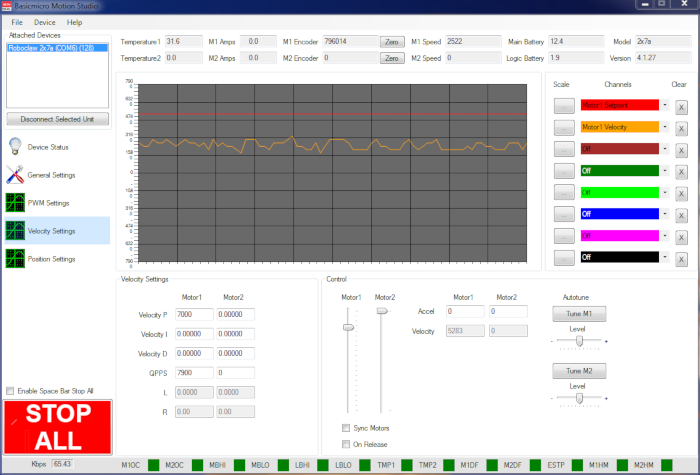
Figure 1: An example of error between a motor’s speed setpoint and actual value.

Proportional

The proportional part of a PID controller looks at the current error and tries to compensate by correcting that error. A proportional value that is too high will cause the system to react too quickly and to overshoot the correction leading to a system that oscillates. Too low of a propotional value and the system will not be able to correct the error properly.

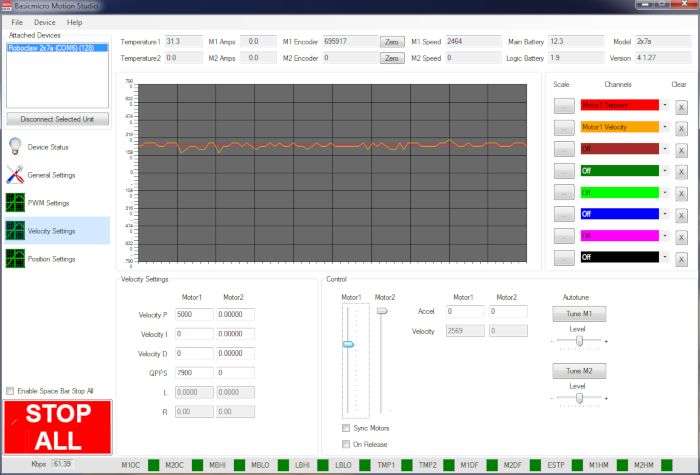
Figure 2: A motor’s speed value oscillating around its setpoint.

Integral

The integral portion of a PID controller looks at the error over time. Any long term trend in the error value are compensated for by the integral correction. As with proportional values of the integral term that are too high can cause the system to oscillate around the setpoint. Integral values that are too long will produce a sluggish response to long term errors.

Derivative

The derivative portion of a PID controller looks at errors in the future. If the proportional or integral correction is likely to overshoot the setpoint the derivative will dampen that reponse and attempt to prevent overshoot and subsequent oscillation. Large values for the derivative can cause the system to react too slowly as it slows the reponse of the proportinal and integral corrections. Values of the derivative that are too low can lead to overshooting of the setpoint.